Stichproben sind fester Bestandteil der Statistik und aufgrund ihrer Praktikabilität eine beliebte Methode für studentische Haus- und Bachelorarbeiten. Sie umfassen eine ganze Bandbreite von Unterarten und Anwendungsgebieten. In diesem Beitrag erhältst du einen Überblick über die Vorgehensweise und ihre verschiedenen Ausprägungen.
Definition: Stichprobe
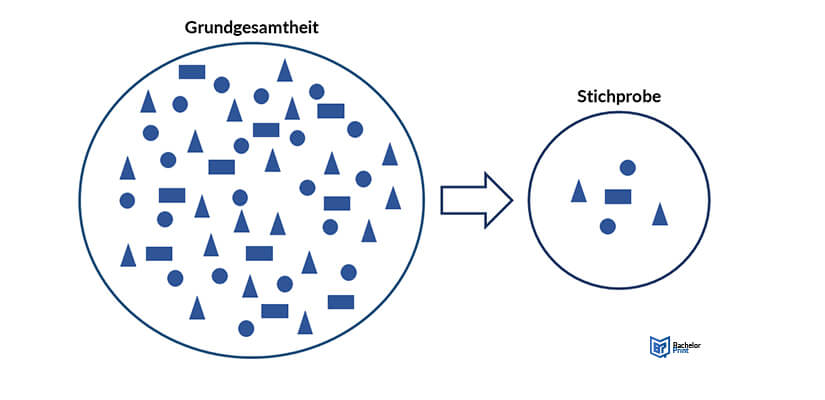
Die Stichprobe ist eine wissenschaftliche Methode, die durch die Teilerhebung von Daten Aussagen über die Grundgesamtheit zulässt. Um die Reliabilität (Verlässlichkeit) dieser Aussagen zu berechnen, kommen verschiedene Formeln aus der Statistik zum Einsatz. Stichproben bieten sich an, wenn es nicht möglich ist eine vollständige Untersuchung der Grundgesamtheit durchzuführen.
Das ist zum Beispiel der Fall, wenn Aussagen über die Gesamtbevölkerung eines Landes getätigt werden sollen. Die meisten Stichproben entstehen mit dem Anspruch, repräsentativ (für die jeweilige Grundgesamtheit) zu sein, weshalb sie unter bestimmten Bedingungen stattfinden müssen. Je nach Anwendungsgebiet bieten sich unterschiedliche Arten von Stichproben an. Die einzelnen Entitäten, aus denen die Daten der Stichprobe gewonnen werden, heißen „statistische Einheiten“ oder „Merkmalsträger“.
Voraussetzungen
Für die Grundgesamtheit aussagekräftige Stichproben müssen repräsentativ sein. Das bedeutet, dass sie die Mindeststichprobengröße erfüllen und aus zufällig ermittelten Merkmalsträgern bestehen müssen. Die Mindeststichprobengröße lässt sich anhand der Formel:
[(Konfidenzwert z x Standardabweichung) / Fehlergrenze]
bestimmen. Eine Stichprobe, die keine Aussagen über die Grundgesamtheit treffen soll, sondern anderen Zwecken (zum Beispiel dem Aufspüren neuer Forschungsimpulse) dient, darfst du auch unter willkürlicheren Bedingungen durchführen.
Probabilistische Stichprobe
Bei der Beurteilung von Stichproben ist zuerst zu klären, ob es sich um eine probabilistische oder eine nicht-probabilistische Stichprobe handelt. Probabilistische erlauben Wahrscheinlichkeitsaussagen über die Beschaffenheit der Grundgesamtheit. Sie sind repräsentativ und basieren auf zufällig bestimmten Merkmalsträgern. Ihr Anwendungsgebiet liegt überall dort, wo zuverlässige Aussagen über Grundgesamtheiten von Nöten sind. Darunter fallen zum Beispiel Wahlumfragen, Studien über die Eigenschaften einer Pflanzenart, über die gesundheitliche Verfassung der Bevölkerung etc. Probabilistische unterliegen hohen Auflagen, um ihrem repräsentativen Anspruch gerecht zu werden. Es wird zwischen vier Unterarten der probabilistischen Stichprobe unterschieden:
- einfache Zufallsstichprobe
- mehrstufige Zufallsstichprobe
- geschichtete Zufallsstichprobe
- Klumpenstichprobe
Einfache Zufallsstichprobe
Eine einfache Zufallsstichprobe entnimmt einzelne Merkmalsträger aus der Grundgesamtheit. Alle potenziellen Merkmalsträger haben die gleiche Wahrscheinlichkeit, Teil der Stichprobe zu werden.
Mehrstufige Zufallsstichprobe
Eine Zufallsstichprobe ist mehrstufig, wenn sie das zufallsbasierte Auswahlverfahren der Merkmalsträger in Form mehrerer Durchläufe gestaltet
Geschichtete Zufallsstichprobe
Eine geschichtete Zufallsstichprobe erlaubt die Vorbestimmung von Merkmalen. Dadurch lässt sich der Bereich, aus dem die Daten bezogen werden, eingrenzen.
Klumpenstichprobe
Bei der Klumpenstichprobe werden keine einzelnen Merkmalsträger ausgewählt. Stattdessen sind sie in Gruppen unterteilt. Der Zufall entscheidet über die Auswahl der Gruppe, die in ihrer Gesamtheit herangezogen wird.
Nicht-probabilistische Stichproben
Nicht-probabilistische Stichproben verwenden kein Zufallsprinzip, um ihre Merkmalsträger zu bestimmen. Sie werden subjektiv nach vordefinierten Relevanzkriterien ausgewählt. Dadurch erlauben sie keine zuverlässigen Aussagen über die Grundgesamtheit, können jedoch Aufschluss über besondere Phänomene bieten und neue Forschungsfragen motivieren. Nicht-probabilistischen Stichproben sind:
- Quotenstichprobe
- theoretischen Stichprobe
- Ad-Hoc-Stichprobe
Quotenstichprobe
Eine Quotenstichprobe setzt voraus, dass die untersuchten Merkmalsträger zu festgelegten Quoten bestimmte Eigenschaften erfüllen. Wenn trotz der Quotenregelung (im Rahmen der quotierten Gruppen) eine zufällige Auswahl der Merkmalsträger stattfindet, handelt es sich in Teilen um eine probabilistische Quotenstichprobe. Wird die Zufallsauswahl gänzlich durch die Festlegung der quotierten Gruppen ersetzt, ist die Stichprobe nicht-probabilistisch.
Theoretische Stichprobe
Die theoretische Stichprobe wählt gezielt Merkmalsträger, an denen die zu untersuchende Eigenschaft besonders deutlich oder in besonders geringem Umfang in Erscheinung tritt. Ferner wird nach sehr ähnlichen und betont-verschiedenen Fällen gesucht. Auf diese Weise wird Schritt für Schritt das Spektrum der Messwerte abgesteckt.
Ad-hoc-Stichprobe
Ad-Hoc-Stichproben entstehen auf der Grundlage einer bestehenden Situation und der Gelegenheit, diese unmittelbar verwenden und auswerten zu können. Wenngleich Ad-Hoc-Stichproben sich nicht dazu eignen, auf die Allgemeinheit zu schließen, liefern sie wichtige Anhaltspunkte für weitere Forschungsprojekte.
Stochastische Schreibweisen
Um die erhobenen Daten stochastisch einzupflegen und die Aussage(-kraft) wissenschaftlich fundiert angeben zu können, kommen mehrere Formeln zum Einsatz. In diesen Formeln steht ein großgeschriebenes N für die Größe der Grundgesamtheit und ein kleingeschriebenes n für die Anzahl der Merkmalsträger innerhalb der Stichprobenziehung. Darüber hinaus beziehen sich Variablen, die mit griechischen Buchstaben angegeben sind, auf die Grundgesamtheit und Variablen mit lateinischen Buchstaben auf die Stichprobe.
Häufig gestellte Fragen
Es ist eine unter bestimmten Bedingungen gesammelte Menge von Daten, die Teil einer (Grund-)Gesamtheit ist. Sie wird genutzt, um Aussagen über diese Gesamtheit zu treffen.
Die Grundgesamtheit ist die vollständige Anzahl von Entitäten (Merkmalsträgern), über die im Rahmen einer Studie Aussagen getroffen werden. Dies können zum Beispiel die Gesamtbevölkerung eines Staates, alle Exemplare einer Spezies oder alle Unternehmen eines bestimmten Wirtschaftszweiges sein.
Um den Mindestumfang für repräsentative Stichproben zu berechnen, kann die Formel [ (Konfidenzwert z x Standardabweichung) / Fehlergrenze] verwendet werden.
Sie ist eine Methode, von der du auch ohne großes Forschungsteam leicht Gebrauch machen kannst. Stichproben sind daher ein gutes Mittel, um dein handwerkliches Können in einer wissenschaftlichen (Bachelor-)Arbeit unter Beweis zu stellen.
- Zufallsstichprobe
- Geschichtete Stichprobe
- Klumpenstichprobe
- Systematische Stichprobe
- Quotenstichprobe
- Gelegenheitsstichprobe
- Urteilsstichprobe
- Schneeballstichprobe