
Egal ob in der Medizin, Wirtschaft oder in der Psychologie – überall werden geeignete Methoden der Statistik verwendet, um aus relevanten Daten aussagekräftige Rückschlüsse zu ziehen. Die Grundlage vieler empirischer Untersuchungen bildet die Regression – sie ermöglicht, Zusammenhänge von Variablen zu analysieren und Vorhersagen über zukünftige Entwicklungen zu treffen.
Definition: Regression
Das Verfahren zählt zu den statistischen Zusammenhangsmaßen und wird angewandt, um Beziehungen zwischen zwei oder mehreren Variablen zu analysieren und deren zukünftige Entwicklung vorauszusagen.
Bei der Methode wird der Einfluss von mindestens einer unabhängigen (Erklär-)Variable (x) auf eine abhängige (Ziel-)Variable (y) zu untersucht.
Hierbei wird ein mathematisches Modell erstellt, um auszusagen, inwiefern Veränderungen der unabhängigen Variable auch Veränderungen in der abhängigen Variable hervorrufen. Somit können Art und Stärke eines Zusammenhangs in Zahlen ausgedrückt, Hypothesen getestet und Prognosen auf Basis des Modells aufgestellt werden.
Das Verfahren ist gerade in den Wirtschafts-, Sozial- und Ingenieurwissenschaften sehr bekannt und wird regelmäßig genutzt, um die Auswirkungen von bestimmten Variablen auf andere nachzuvollziehen und relevante Schlussfolgerungen für die Zukunft zu ziehen.
Modelle
Es gibt unterschiedliche Analysemodelle, um auf individuelle Datensätze und Fragestellungen einzugehen. Im Folgenden werden die gängigsten Modelle in der Praxis erläutert.
Einfache lineare Regression
Hierbei handelt es sich um das grundlegendste Modell, welches die Beziehung zweier quantitativer Variablen (z. B.: Größe, Gewicht, Alter oder Einkommen) beschreibt. Dabei gilt es, einen linearen Zusammenhang zwischen einer unabhängigen und einer abhängigen Variablen zu analysieren. Wenn man sagt, dass zwei Variablen eine positive lineare Korrelation aufweisen, so meint man, dass wenn eine Variable zunimmt, auch die andere Variable zunimmt und umgekehrt ebenso.
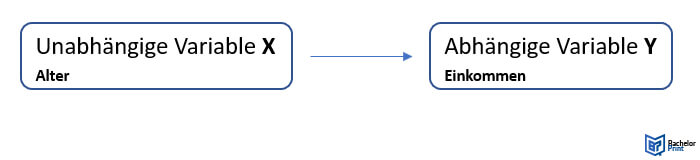
Zum Beispiel kann das Modell verwendet werden, um zu sehen, wie sich mit steigendem Alter das Einkommen verändert.
Multiple lineare Regression
Bei der multiplen Variante wird der simultane Einfluss von mehreren unabhängigen Variablen auf eine abhängige Variable analysiert. Da in vielen Wissenschaften nur selten monokausale Beziehungen untersucht werden, ist das multiple Modell ein unverzichtbares Hilfsmittel in der Forschung.
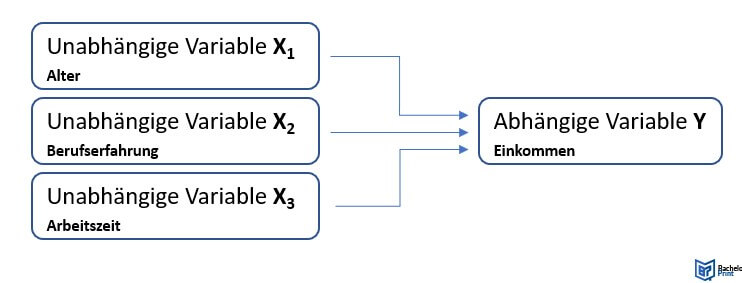
Dieses Modell kann beispielsweise in der Arbeitsmarktforschung nützlich sein, um zu verstehen, wie verschiedene Faktoren (wie Alter, Berufserfahrung und Arbeitszeit, etc.) das Einkommen beeinflussen.
Logistische Regression
Dieses Modell wird verwendet, wenn die abhängige Variable kategorisch ist, insbesondere wenn sie binär ist (also zwei Kategorien hat, wie ja/nein oder Erfolg/Misserfolg). Im Gegensatz zum linearen Modell, die die tatsächliche Ausgabe vorhersagt, wird bei der logistischen Variante die Wahrscheinlichkeit vorhergesagt, dass eine Beobachtung zu einer bestimmten Kategorie gehört.
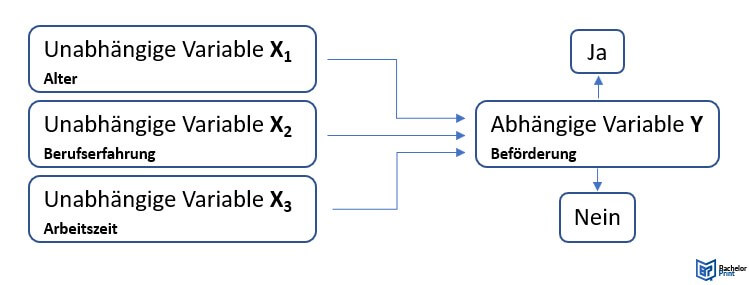
Dieses Modell kann zum Beispiel im beruflichen Kontext verwendet werden, um vorherzusagen, ob einem Mitarbeiter aufgrund seines Alters, Berufserfahrung und der geleisteten Arbeitszeit eine Beförderung zusteht oder nicht.
Methodik
Zentraler Teil der Regression ist die Methode der kleinsten Quadrate (englisch: Ordinary Least Squares, kurz: OLS), die dazu dient, die Koeffizienten zu schätzen, welche die Beziehung zwischen der unabhängigen und der abhängigen Variable am besten beschreiben.
Die Methode basiert auf der Minimierung der Summe der quadrierten Differenzen (oder „Fehler“) zwischen den tatsächlichen Werten der abhängigen Variablen und den von der Regressionsgleichung vorhergesagten Werten. In anderen Worten, sie findet die „beste“ Linie, die durch die Datenpunkte verläuft.
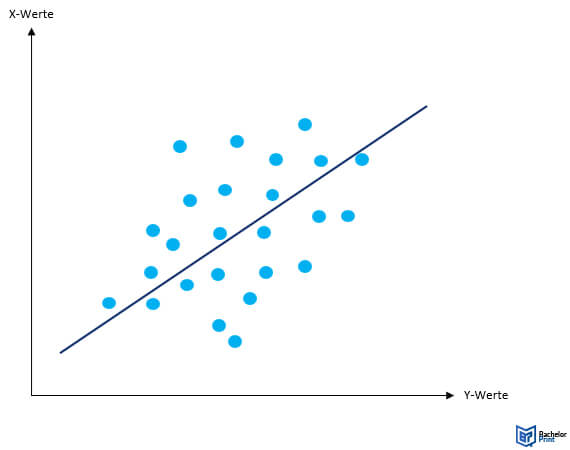
Analysetools
Es gibt zahlreiche Software- und Programmiersprachen, die zur Durchführung einer Regressionsanalyse verwendet werden können. Die Wahl des Tools hängt von vielen Faktoren ab, einschließlich der eigenen Anforderungen, Erfahrung und Kenntnissen in der Programmierung, dem zur Verfügung stehenden Budget und den Normen im jeweiligen Fachgebiet. Hier die bekanntesten Tools im Vergleich:
| Tool | Positive Merkmale | Negative Merkmale |
| R | + Freie Software + Sehr flexibel und leistungsstark + Zahlreiche Pakete für alle Analysearten + Hervorragende Grafikmöglichkeiten |
- Steile Lernkurve |
| Python | + Freie Software + Für andere Arten der Datenverarbeitung ist eine Einbindung der Analyse in größere Codes möglich + Einfacher zu lernen als R |
- Geschwindigkeit der Ausführung kann langsamer sein |
| SPSS | + Userfreundliche grafische Oberfläche + Umfangreiche Optionen zur Datenaufbereitung und -manipulation |
- Kostenintensive Software - Möglichkeiten zur Anpassung und Automatisierung sind begrenzter |
| Excel | + Intuitive und den meisten geläufige Benutzeroberfläche + Breite Verfügbarkeit für die Masse + Grundlegende Analysefunktionen sind enthalten + Diagramme und Grafiken können leicht erstellt werden |
- Begrenzte Auswahl an statistischen Funktionen - Kann bei größeren Datensätzen an seine Grenzen stoßen - Mangel an Reproduzierbarkeit von Analyseprozessen |
Häufig gestellte Fragen
Es handelt sich um ein statistisches Verfahren zur Modellierung und Analyse der Beziehung von einer abhängigen Variable und einer oder mehreren unabhängigen Variablen.
Eine Regression wird in Bereichen verwendet, welche regelmäßig Umgang mit empirischen Daten haben. Sie kann verwendet werden, um Vorhersagen zu machen, Trends zu erkennen, oder um die Auswirkungen von Änderungen einer unabhängigen Variable auf die abhängige Variable zu verstehen.
Die Methode der kleinsten Quadrate basiert auf der Minimierung der Summe der quadrierten Differenzen zwischen den tatsächlichen Werten der abhängigen Variablen und den von der Regressionsgleichung vorhergesagten Werten.
Dies hängt von der Art der Daten und der Fragestellung ab. Jedoch kann man generell zwischen den Modellen der einfachen linearen, multiplen linearen sowie der logistischen Regression unterscheiden.
Beim einfachen linearen Modell wird nur eine einzige unabhängige Variable zur Erklärung einer abhängigen Variable herangezogen. In der multiplen linearen Variante werden mehrere unabhängige Variablen zur Vorhersage der abhängigen Variable betrachtet.