Inhaltsverzeichnis
Der Korrelationskoeffizient gibt die Stärke der linearen Beziehung zwischen zwei oder mehr Variablen an und findet oftmals Verwendung in der Statistik.
Wir zeigen dir, anhand von einigen Beispielen, wie du ihn berechnen und auswerten kannst. Zudem erfährst du, wie du den Korrelationskoeffizient mit Excel, Google Tabellen und SPSS errechnen kannst.
Definition: Korrelationskoeffizient
Der Korrelationskoeffizient nach Pearson kann Werte von -1 bis 1 annehmen und wird durch r symbolisiert. Bei einem Wert von 0 ist zwar keine lineare Abhängigkeit gegeben, die einzelnen Merkmale können jedoch in nichtlinearer Weise voneinander abhängen. Die Werte 1 und -1 stellen sogenannte perfekte Korrelationen dar: In beiden Fällen verändern sich beide Variablen in demselben Maße, allerdings in verschiedenen Richtungen.
Der Korrelationskoeffizient r ist das Ergebnis der Korrelationsanalyse. Bei dieser handelt es sich um ein statistisches Verfahren, das den Zusammenhang zwischen zwei Variablen erläutert. Der Korrelationskoeffizient enthält Informationen über die Stärke ebenso wie über die Richtung des Zusammenhangs. Wenn der Wert einer Variable steigt bzw. fällt, tut es auch der Wert der anderen Variable.
Berechnung des Korrelationskoeffizienten
Es gibt verschiedene Möglichkeiten, um den Korrelationskoeffizienten zu berechnen. Hier stellen wir die gängigsten Methoden vor und erklären diese genauer.
Korrelationskoeffizient mit Formel berechnen
Man kann den Korrelationskoeffizienten r mithilfe der entsprechenden Formel berechnen:
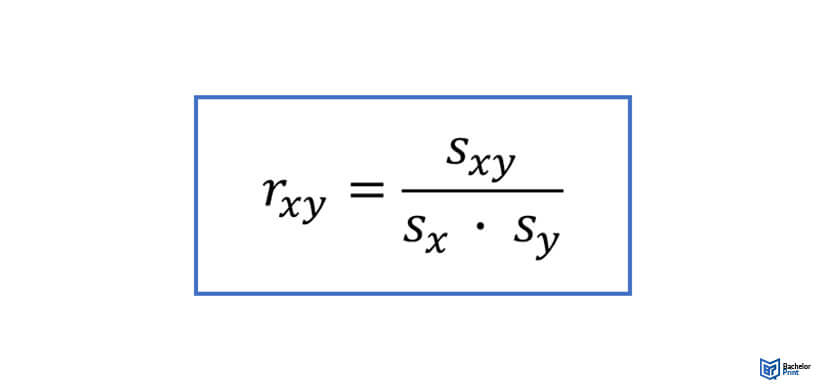
sxy bezeichnet die Kovarianz der Variablen x und y
sx ist die Standardabweichung der Variable x
sy ist die Standardabweichung der Variable y
Berechnung des Korrelationskoeffizienten mit Excel oder Google Tabellen
Man kann den Korrelationskoeffizienten auch ganz einfach mithilfe von Excel oder Google berechnen. In Excel gibt man in einer leeren Zelle die Formel = KORREL () an, in Google-Tabellen = CORREL (). Man wählt die Daten aus den entsprechenden Spalten aus und trennt sie durch ein Semikolon. Zum Schluss erhält man den Wert des Korrelationskoeffizienten.
Berechnung des Korrelationskoeffizienten mit SPSS
Der Korrelationskoeffizient lässt sich im Statistikprogramm SPSS berechnen. Im Menü klickt man auf „Analysieren“, „Korrelation“ und „Bivariat“. Im neuen Fenster wählt man die Variablen aus, die man analysieren möchte. „Pearson“ sollte markiert sein, da man die lineare Korrelation erforschen möchte. Um die Analyse durchzuführen, muss man auf „OK“ klicken.2
Interpretation des Korrelationskoeffizienten
Der Wert des Korrelationskoeffizienten liegt zwischen -1 und 1. Beide Extreme drücken eine perfekte Korrelation aus. Beträgt der Korrelationskoeffizient 0, besteht kein linearer Zusammenhang zwischen den Variablen. Es kann jedoch sein, dass ein nichtlinearer Zusammenhang zwischen den Variablen besteht. Bis 0,1 bzw. -0,1 besteht ein schwacher Zusammenhang, von 0,1/-0,1 bis 0,5/-0,5 ist der Zusammenhang mittelstark, von 0,5/-0,5 bis 1 /-1 ist der Zusammenhang zwischen den beiden Variablen stark.
Zusammenhangsrichtung: positive oder negative Korrelation
Ist der Wert des Korrelationskoeffizienten positiv, besteht eine positive Korrelation. Ein negativer Korrelationskoeffizient weist auf eine negative Korrelation hin. Ein positiver Korrelationskoeffizient kann Werte von 0 bis 1 einnehmen, während ein negativer Korrelationskoeffizient zwischen -1 und 0 liegt. Eine positive Korrelation besagt, dass die Werte beider Variablen linear steigen.
Zusammenhangsstärke
Wenn wir den r-Wert berechnet haben, müssen wir ihn auch interpretieren. Eine Möglichkeit ist die Einteilung nach Cohen:
- -0,1 bis 0 und 0 bis 0,1: schwacher Zusammenhang
- 0,1/-0,1 bis 0,5/-0,5: mittlerer Zusammenhang
- 0,5/-0,5 bis 1/-1 bis: starker Zusammenhang
Voraussetzungen zur Bestimmung
Der Korrelationskoeffizient kann nur dann berechnet werden, wenn folgende Voraussetzungen zutreffen:
- Es liegt ein metrisches Skalenniveau vor.
- Die Daten sind normalverteilt.
- Es besteht linearer Zusammenhang zwischen den Variablen.
Metrisch skalierte Daten weisen quantifizierbare Abstände und eine natürliche Reihenfolge auf. Als Beispiele gelten die Wassertiefe in Zentimetern oder die Zeitdauer in Sekunden.
Die Normalverteilung wird auch als Gauß-Verteilung bezeichnet. In ihrer grafischen Darstellung erinnert sie an eine Glocke. Der Kurvenverlauf ist symmetrisch, wobei Median und Mittelwert identisch sind. Man kann sagen, dass die Körpergröße in Deutschland normalverteilt ist.3
Liegt ein linearer Zusammenhang vor, bewegen sich die Variablen mit einer konstanten Rate in dieselbe Richtung. Nehmen beispielsweise beide Variablen mit verschiedenen Raten zu, spricht man von einer monotonen statt einer linearen Beziehung.
Koeffizient in wissenschaftlichen Arbeiten
Der Korrelationskoeffizient wird im Ergebniskapitel der wissenschaftlichen Arbeit beschrieben.
Häufig gestellte Fragen
Der Korrelationskoeffizient drückt die Stärke des Zusammenhangs zwischen zwei linearen Variablen aus. Dabei kann dieser Zusammenhang positiv oder negativ sein.
Ein hoher Korrelationskoeffizient liegt zwischen 0,5/-0,5 und 1/-1.
Ist der r-Wert 0, besteht kein linearer Zusammenhang zwischen den Variablen. Allerdings kann ein nichtlinearer Zusammenhang vorliegen.
Ein positiver Korrelationskoeffizient drückt das Prinzip „wenn mehr, dann mehr“ aus, wohingegen ein negativer Korrelationskoeffizient „wenn weniger, dann mehr“ steht.
Korrelationsanalysen werden in vielen verschiedenen Bereichen durchgeführt. Besonders erwähnenswert sind Anlageportfolios, bei denen das Gesamtrisiko umso geringer ist, je weniger die einzelnen Anlagen miteinander korrelieren.
Quellen
1 Universität Duisburg-Essen: Korrelation und Kausalität, in: uni-due.org, o.D., [online] https://www.uni-due.de/dataedu/korrelation-vs-kausalitat/ (21.01.2023)
2 Universität Zürich: Korrelation nach Bravais-Pearson, in: methodenberatung.uzh.ch, 21.03.2022, [online] https://www.methodenberatung.uzh.ch/de/datenanalyse_spss/zusammenhaenge/korrelation.html (21.01.2023)
3 Universität zu Köln: Gender, in: Universität Leipzig Schreibportal, o.D., [online] https://lehre.idh.uni-koeln.de/lehrveranstaltungen/sosem21/basissysteme-der-informationsverarbeitung-2-bsi-4/statistik/normalverteilung/#:~:text=Eine%20Normalverteilung%20(Gau%C3%9F%2DVerteilungskurve%2C,fallen%20also%20auf%20einen%20Wert.&text=liegen. (21.01.2023)